🇫🇷 Etude d’un dataset aléatoire
Classification
Analyse exploratoire
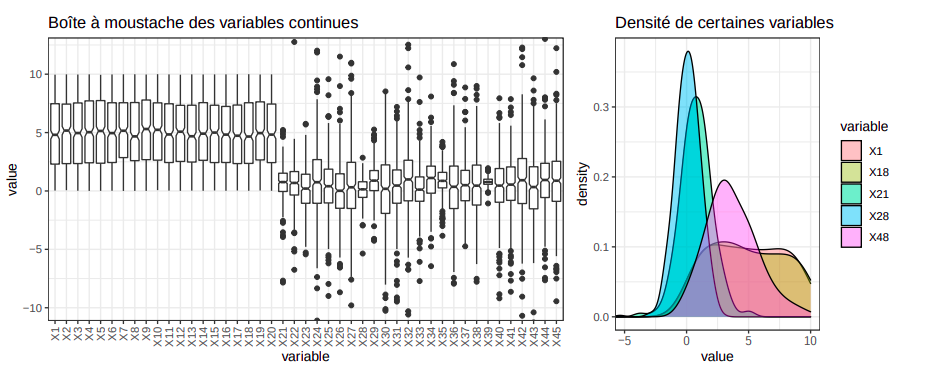
L’objectif de ce travail est de proposer le meilleur classifieur possible à partir de 500 observations, capable de distinguer trois classes (noté 1, 2 et 3) de proportion initiale inégale ($π_1 = 0.18, π_2 = 0.442, π_3 = 0.378$). Comme le jeu de données est synthétique, il est impossible d’attribuer une signification à chaque variable. Tout de même, les variables se distinguent clairement en trois groupes:
X1 à X20, suivant une distribution bimodale continue d’espérance E[X] = 5 et de variance relativement faible:
- X21 à X45, suivant une loi normale continue d’espérance E[X] = 0 et de variance elevée
- X46 à X50, avec une distribution discrète positive centrée aux alentours de E[X] = 3.7
Feature selection
Puisque nous avons une quantité importante de variable par rapport aux nombres d’observations (1/10), il serait judicieux d’appliquer des méthodes de réduction de dimensions si possible.Comme l’analyse en composantes principales ne fonctionne qu’avec les données quantitatives, nous posons l’hypothèse que les variables X45 − X50 sont quantitatives. Suite à cette analyse, nous observons qu’il faut garder 40 variables afin de préserver 90% de la variance expliquée. Il y a donc peu d’intérêt d’appliquer cette réduction.
KNN
L’algorithme des KNN consiste à affecter à un individu la classe dominante dans son voisinnage. En supprimant les variables qualitatives (X46 à X50), une LOOCV permet de montrer que le nombre de voisin optimal est k = 15 avec un taux d’erreur de classification à 0.572. Ce taux d’erreur élevé peut s’expliquer par plusieurs facteurs:
- dans l’espace de départ les centres d’inertie des classes sont proches les unes des autres
- la proportion inégale des classes pousse le classifieur à toujours choisir la classe 2
- la distance euclidienne utilisée par défaut est très sensible à un nombre élevé de prédicteurs
Les techniques d’analyses discriminantes vues en cours peuvent être facilement étendues à des problèmes de classification multi-classe car l’appartenance à une classe revient à trouver la probabilité à posteriori maximale pour l’individu donné.
Analyse discriminante
Puisque les frontières construites par la LDA sont linéaires et que dans l’espace de départ, il n’y a pas d’hyperplans discriminants apparents, la qualité du classifieur qui en résulte est médiocre avec un taux d’erreur de classification de 0.42.
De plus, un test de Barlett sur le jeu de données permet de rejetter l’hypothèse nulle d’homoscédasticité entre les différentes classes à un niveau de confiance à $2.2e^{−16}$. Nous pouvons donc tenter d’éliminer cette hypothèse en utilisant l’analyse discriminante quadratique (QDA). Avec une validation croisée à 10 plis, nous obtenons les taux d’erreur de classification suivant:
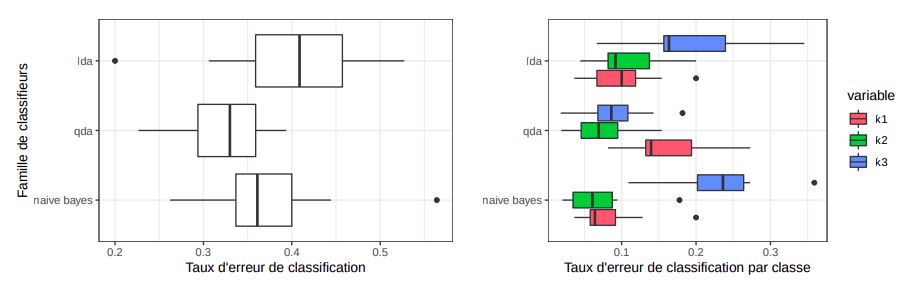
La variance élevée observée d’un modèle QDA par rapport à un modèle LDA peut s’expliquer par le fait qu’il doit estimer plus de paramètres sur un échantillon de taille relativement faible. De plus, la QDA fait moins d’erreur de classification pour les individus de classe 3 et légèrement plus d’erreur pour les individus de classe 1, ce qui donne en générale un meilleur modèle sachant que $π_3 > π_1$.
Les modèles étudiées ci-dessus doivent estimer un nombre de paramètres proportionnel aux nombres de variables et de classes. Or, dans notre cas, avec 50 variables et 3 classes, la QDA doit estimer 3977 paramètres et la LDA 1427, ce qui va faire exploser la variance des modèles obtenus.
Pour palier à ce problème, en supposant l’indépendance des prédicteurs conditionnellement à leurs classes, on peut construire un classifieur bayésien naïf avec moins de paramètres à estimer et donc plus adapté à notre nombre de variables. Malgré sa simplicité, le bayésien naïf offre une meilleure performance générale que la LDA et un meilleure classification de la classe 1 que la QDA.
Régularisation
L’analyse discriminante régularisée (RDA) permet de trouver un compromis entre le biais élevé des LDA et la variance élevée des QDA. Au lieu d’estimer une matrice de variance commune (\hat{\Sigma}) comme dans la LDA ou des matrices de variance ($\hat{\Sigma}_k$) pour chaque classe, elle construit une matrice de covariance régularisée de la forme: $\hat{\Sigma}_k(\lambda) = (1 − \lambda)\hat{\Sigma}_k + \lambda\hat{\Sigma}$. Lorsque $\lambda \rightarrow 0$, le classifieur se rapproche d’une QDA et lorsque $\lambda \rightarrow 1$, le modèle tends vers une LDA.
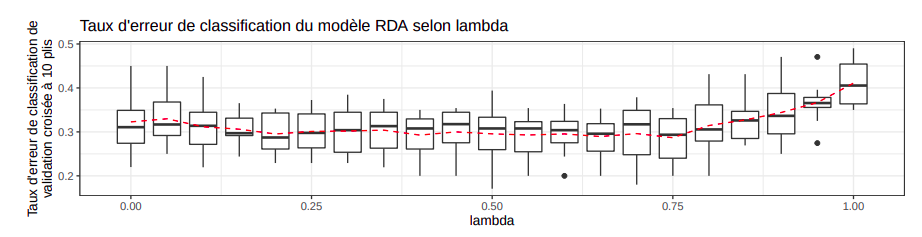
En faisant une recherche systèmatique dans l’espace des \lambda, on peut conclure qu’un coefficient de régularisation $\lambda \in [0.50, 0.55]$ donne le modèle optimal qui favorise légèrement l’homoscédasticité des variances. L’analyse RDA admet aussi un coefficient $\gamma$ qui permet de régulariser $\hat{\Sigma}$ selon la formule $(1 − \gamma)\hat{\Sigma} + \gamma\sigma^2 I_p$.
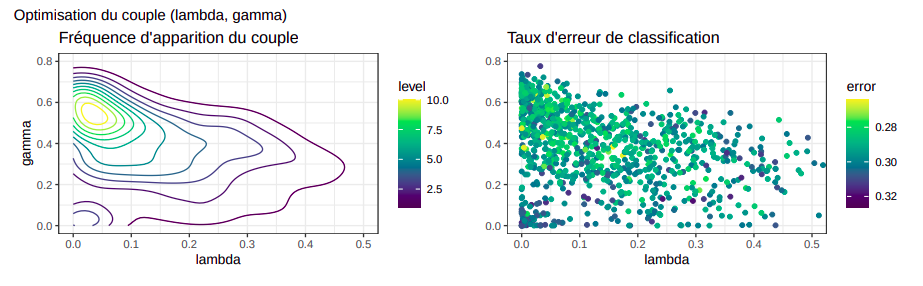
La fonction rda dans la librairie klaR qui permet d’optimiser les deux paramètres n’est pas stable pour les
jeu de données de petite taille. Nous pouvons lancer plusieurs itérations et identifier les zones optimales
où se trouvent le plus fréquemment les solutions et où le taux d’erreur de classification est le plus faible.
Nous trouvons donc que les couples de paramètres optimales sont comprises entre $\lambda \in [0.04, 0.05]$ (ce qui
correspond à une QDA) et $\gamma \in [0.50, 0.055]$.
Stepwise selection
La fonction stepclass de la librairie klaR adapte la stepwise selection à la classification et donne directement
le sous-ensemble de prédicteur optimal qui garantit le taux d’erreur de classification issu d’une validation
croisée le plus faible. Nous observons donc que cette sélection des variables échange la performance moyenne
du classifieur pour réduire la variance du modèle
Régression Logistique
Contrairement à l’analyse discriminante linéaire, la régression logistique est un modèle plus robuste qui ne présume pas que les prédicteurs suivent une distribution gaussienne multidimensionnelle et fonctionne avec les variables qualitatives. Tout de même, en appliquant une régression multinomiale sur l’ensemble du jeu de données, le taux moyen d’erreur de classification issue d’une validation croisée à 10-plis est aux alentours de 0.45 et dépasse celui obtenu avec une LDA.
Pour améliorer cette performance, il serait judicieux d’éliminer les prédicteurs “redondants” qui sont trop fortement correlés entre eux puis les prédicteurs à effet négligeable sur le modèle. La matrice de correlation des données, elle, révèle aucune correlation forte entre les prédicteurs donc il faut remettre en question la significativité des variables. Les méthodes de régularisation qui suppriment les coefficients négligeables tel que le lasso ou qui les pénalisent tel que l’elastic net peuvent résoudre ce problème
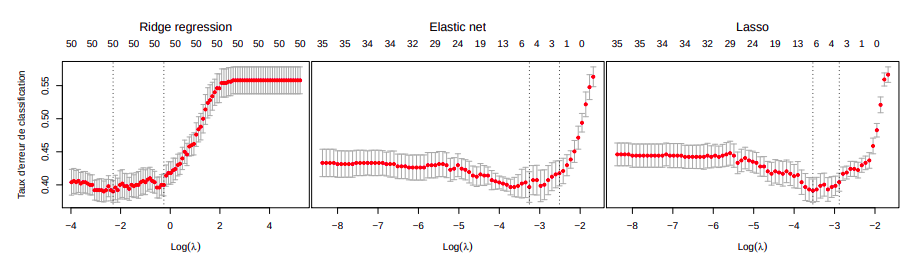
Avant d’appliquer la régularisation, les variables quantitatives sont centrées et réduites afin d’augmenter la stabilité des estimations des coefficients et donc du modèle puis rattachées aux variables qualitatives. Nous observons alors que la régularisation réduit de manière non négligeable le taux d’erreur de classification de la régression logistique.
En prenant la valeur de lambda la plus régularisée selon la règle du 1-se, les coefficients $\beta$ obtenus entre le lasso et l’elasticnet sont proches et révèlent l’importance des variables qualitatives dans la classification des individus 1 et 2.
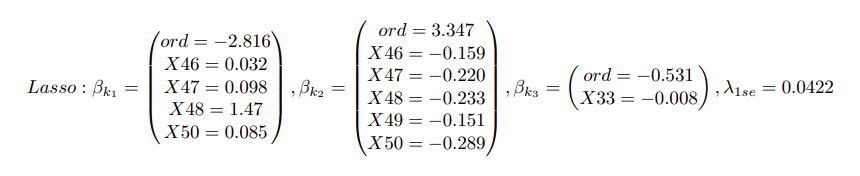
Arbres et forêts aléatoires
En régularisant l’arbre de décision par post-élagage, nous obtenons une erreur de validation croisée optimale pour un arbre de profondeur 5 de 0.46. Avec la forêt aléatoire, nous obtenons un modèle de variance plus faible mais fortement biaisé (la forêt décide rarement pour la classe 1) avec une erreur OOB de 0.394. Même après avoir augmenté le poids de cette classe dans l’apprentissage, ce problème n’est pas résolu.
Conclusion
| Modèle | Taux d’erreur de classification |
|---|---|
| KNN | 0.572 |
| LDA | 0.616 |
| LDA subset | 0.375 |
| QDA | 0.321 |
| QDA subset | 0.314 |
| RDA | 0.303 |
| RDA subset | 0.303 |
| Logit | 0.450 |
| Logit Ridge | 0.386 |
| Logit Elasticnet | 0.376 |
| Logit Lasso | 0.376 |
| Random Forest | 0.394 |
Le modèle RDA est donc optimal pour classifier ce jeu de données. Dans nos futurs travaux, il serait intéressant d’adresser le déséquilibre des classes (avec du under-sampling ou du SMOTE) et de tester d’autre méthodes supervisées (SVM ou SGD).
Régression
L’objectif de ce travail est de proposer la meilleure régression sur la variable y (E[y] = 161.65) à partir d’un échantillon de 500 réalisations de 100 variables. Similairement au problème de classification, aucune une signification peut être attribuer à chaque variable. Tout de même, contrairement aux données de classification, l’ensemble des variables sont quantitatives continues d’espérance communes proches de E[X] = 5 qui est constitué de deux groupes:
- un groupe majoritaire suivant une distribution bimodale continue
- une minorité (dont notamment X50, X65) qui suit peut-être une distribution multimodale (k = 3)
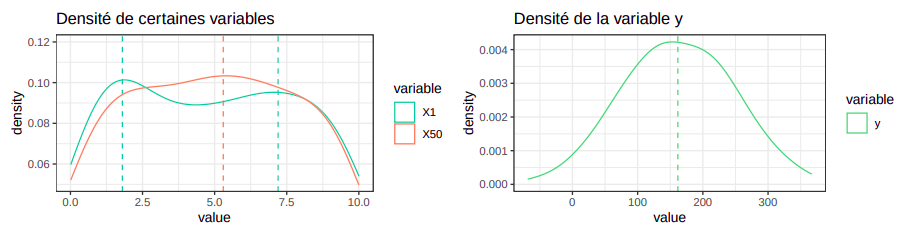
Quant aux réalisations de la variable à prédire, elle, suit clairement une loi normale avec $\hat{\mu} = 161.65$ et $\hat{\sigma} = 82.67529$.
Feature selection
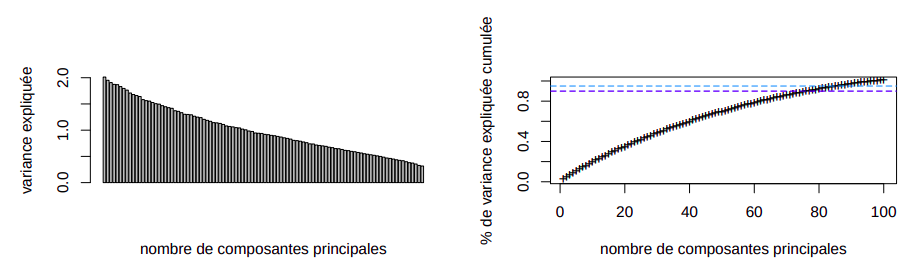
Pour ce jeu de données, le problème du rapport entre le nombre de prédicteurs et le nombre d’indivdus est encore plus prononcé (1/5). D’où la nécessité de réduire si possible la dimension par PCA. Tout de même, afin de maintenir 90 de la variance expliquée cumulée, 80 axes doivent être maintenus et la méthode du coude ne révèle pas non plus un nombre de composantes principales optimal.
KNN
L’algorithme des knn se fonde sur un vote majoritaire des individus dans le nuage. Cette proximité se définit
par une distance (euclidienne par défaut dans l’implémentation dans la librairie MASS) commun par rapport à
tous les dimensions. Or, dans un jeu de données non standardisés, les échelles entre les dimensions peuvent différer. D’où, la nécessité de normaliser (centrage et réduction) au préalable les données. Avec ce prétraitement sur l’ensemble des prédicteurs (y exclu), l’erreur quadratique moyenne du modèle avec le nombre de voisins optimal obtenue par validation croisée imbriquée améliore de manière négligeable de 5099.594 à 5082.458. Malgré cette performance médiocre, ceci confirme l’observation que les données initiales sont relativement “homogènes” (moyenne et écart-type similaire).
Modèles linéaires
De première vue, il est très probable que y soit une combinaison linéaire des différents prédicteurs et donc qu’un modèle linéaire sera optimal pour notre problématique.
Dans un premier temps, nous avons estimé le vecteur des coefficients $\hat{\beta}$ de la régression par la méthode des moindres carrés sur 75 des observations. Le modèle qui en résulte est bien significatif car nous obtenons une pvalue < $2.2e^{−16}$ pour l’hypothèse de nullité de l’ensemble des paramètres.
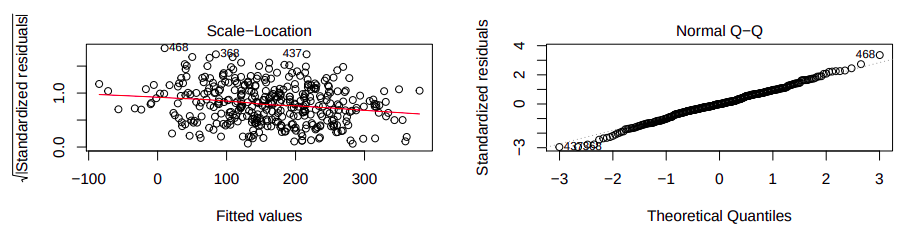
De plus, nous constatons que les résidus ne semble pas suivre une structure particulière et que les résidus standardisés épousent bien le qqplot d’une loi normale. Ceci confirme l’hypothèse de normalité des résidus et nous pouvons donc tenter de faire une validation croisée pour estimer la performance du LSE sur nos données. Nous obtenons donc une bonne erreur quadratique moyenne de 260.1426 pour un modèle relativement simple.
Subset selection
A partir du modèle précédent, une question peut se poser: est-ce qu’il y a certaines variables non significatives ou qui nuisent à la régression? En étudiant l’évolution du coefficient de corrélation $R^2$ en fonction du nombre de prédicteurs pris en compte, la méthode du subset selection permet de montrer que pour maintenir un modèle de performance similaire, il suffit de maintenir 80 variables.
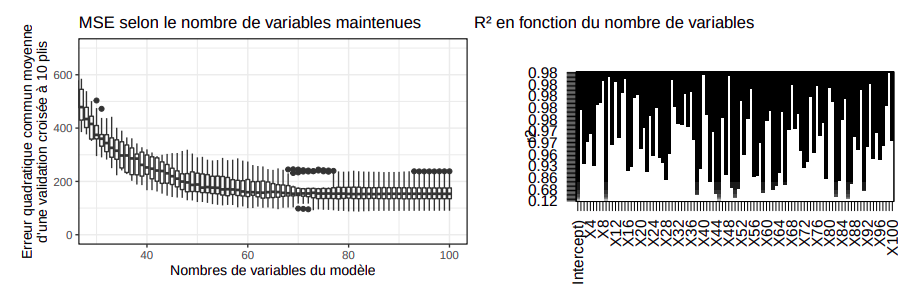
L’usage de cette méthode permet de réduire la variance du modèle obtenu ainsi que la moyenne des erreurs quadratiques observées à 235.1.
Régularisation
Similairement à la régression logistique dans la classification, il est possible de régulariser la régression linéaire en pénalisant les coefficients par la méthode Ridge ou le Lasso. En faisant une validation croisée imbriquée pour optimiser les valeurs de $\lambda$, nous obtenons cette comparaison de la qualité des différentes méthodes de régularisation.
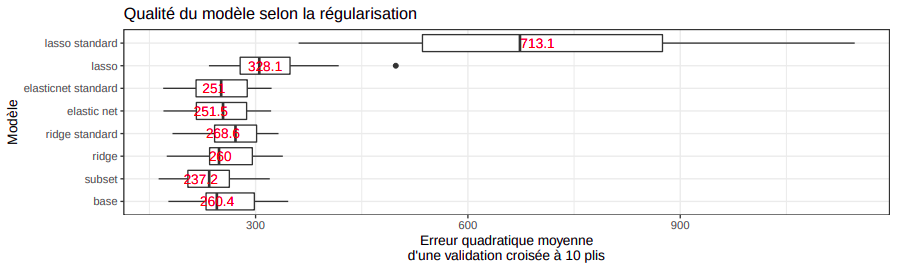
Nous observons donc que parmi les régularisations, le Ridge et le modèle de compromis (Elastic Net) dépassent clairement le lasso en terme de performance. Ceci suggère que le nombre de variables important dans la prédiction de y est important et la suppression de ces variables par lasso n’est pas nécessaire. De plus, nous observons que la standardisation (centrage et réduction) des données activée par défaut dans la fonction glmnet affaiblit le lasso puisqu’elle accélère peut-être trop fortement la contraction des coefficients.
Splines et GAM
Il est possible que la variable à prédire résulte d’une combinaison non linéaire des prédicteurs. Comme nous avons un jeu de données de dimension > 2, deux modèles multidimensionnels ont été abordés en cours:
- Les splines multidimensionnels qui combinent les différentes fonctions de transformation par produit. Avec 100 prédicteurs, il est impossible d’appliquer ce modèle sans sélection préalable à cause du nombre de paramètres à estimer.
- Les modèles additifs généralisés (GAM) qui cherchent 100 fonctions transformant chacun une variable au lieu d’une fonction à 100 dimensions.
En appliquant le gam avec un type de spline unique sur l’ensemble des prédicteurs sans standardisation, nous obtenons les erreur quadratique suivante à l’issu d’une validation croisée à 10 plis:
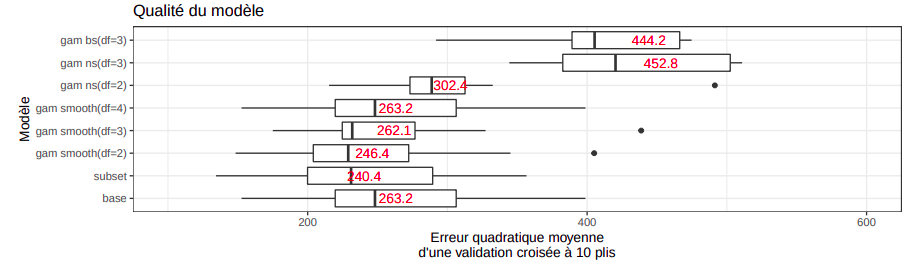
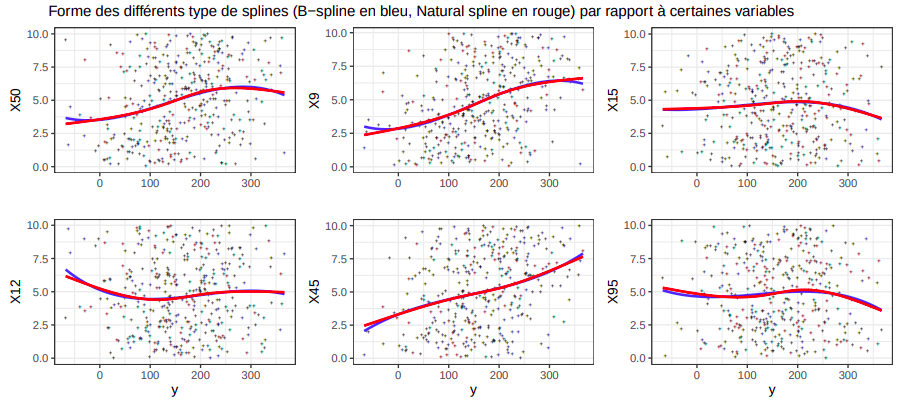
La forme des b-splines cubiques (gam bs(df=3)) et des splines naturels (gam ns(df=3)) sont très similaires
mis à part au niveau des frontières de l’espace de y. Comme le gam est additif, ces similarités s’aggrègent
dans le modèle final et explique la proximité entre les erreurs.
Quant aux smoothing splines avec un degré de liberté de 2, nous obtenons un modèle de performance
relativement proche au subset. En examinant de près ce modèle, nous observons que seulement 68 variables
sont significatives (à l’issu d’une analyse de variance paramétrique) et qu’il n’y aucune transformation de la
prédiction (fonction de lien: identity).
Conclusion
| Modèle | MSE moyenne |
|---|---|
| KNN | 5082.458 |
| Linear Regression (LR) | 260.1426 |
| LR subset selection | 235.1 |
| Ridge regression | 259.8 |
| Elasticnet regularisation | 249.9 |
| Lasso regularisation (without standardisation) | 317.5 |
| GAM (b-spline,df=3) | 429.3 |
| GAM (natural spline, df=2) | 294.8 |
| GAM (smoothing spline, df=2) | 233.2 |
Le GAM constitué uniquement de smoothing spline sur l’ensemble des prédicteurs non standardisés est donc optimal pour notre jeu de données car il donne l’erreur quadratique moyenne minimal ainsi qu’une variance relativement faible.
Dans nos futurs travaux, il serait intéressant d’effectuer une sélection préalable des variables avant le GAM et tester d’autre modèles comme les machines à vecteurs de support (SVM) ou même les splines multidimensionnels (après une réduction de dimension par manifold learning).