Ce travail a été fait avec Marc DAMIE dans le cadre de l’UV IA02

Représentation d’une grille

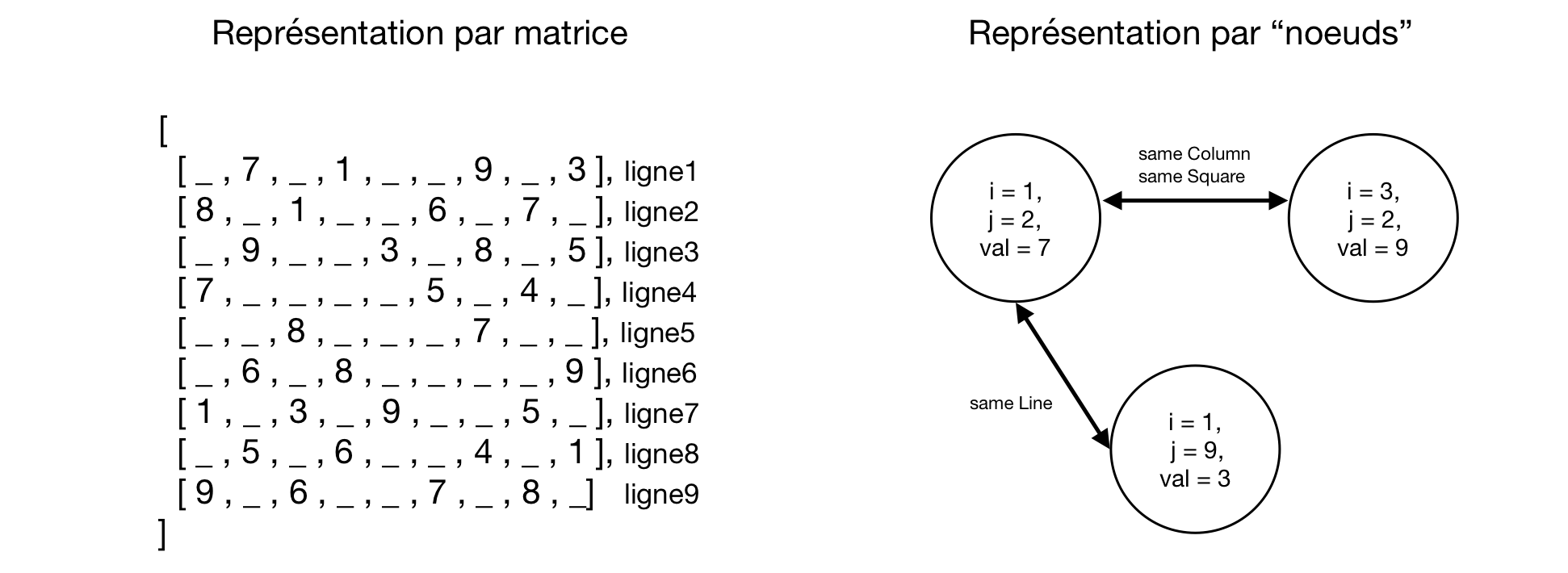
Nous avons décidé de représenter une grille comme étant une “matrice”, c’est-à-dire une liste avec neuf listes imbriquées avec neuf éléments dans chaque liste. Pour la représentation d’une cellule vide, nous avons décidé d’utiliser une variable anonyme _ , la variable anonyme, elle, peut s’unifier avec tout caractère et donc avec 0 (propriété que l’on utilisera pour le programme qui suit). Avec cette structure, nous en tirons les avantages et les inconvénients suivants:

Inconvénients

Avec cette structure, insérer une valeur dans une cellule nécessite un temps de calcul plus important vu que l’on doit parcourir récursivement l’ensemble de la liste (ce qui, dans le pire des cas, engendrait 81 opérations). A ceci, se rajoute le fait que l’accès à une certaine colonne n’est pas directe, ce qui va réduire l’efficacité des tests au cours de la génération de la grille (notamment celui de l’unicité sur une colonne). Finalement, sa performance n’est pas optimale pour les grilles presque vides, vu qu’elle associe à chaque case vide une valeur 0 et peut-être une question sur l’optimisation de l’espace mémoire utilisée.

Avantages

Elle demeurent, néanmoins, plus adaptée que la représentation d’une grille par une base de faits dynamiques (ex; prédicat board(I,J,Val) représentant qu’à la i-ème ligne, j-ème colonne, il y a la valeur Val) car elle permet facilement de tester la validité d’une insertion (le backtracking sur les assertions dynamiques étant presque impossible). Contrairement à la vérification de la validité des colonnes, l’unicité des lignes et des carrées 3x3 peuvent être vérifiées assez rapidement avec cette matrice. La représentation matricielle, elle, simplifie aussi les opérations de propagation (cf Génération de grille) telles que les rotations, les permutations de grilles.

Manipulation de la matrice

Pour manipuler cette structure, nous avons appuyé notre code sur le prédicat element(I,J,B,X). Celui-ci nous permettra d’obtenir l’élément à la position I,J. Il offre une certaine optimisation car on peut obtenir n’importe quel élément en maximum 18 opérations: n a besoin de 9 opérations pour atteindre la 9ième ligne et 9 autres pour atteindre le 9ième élément de celle-ci.

Recherche d’une solution

Génération d’une valeur valide pour une case donnée

La brique de base de notre résolution est de générer pour une case donnée une valeur valide pour la ligne, la colonne et le carré. Par valeur valide, on entend une valeur unique sur la ligne, la colonne et le carré. On utilise alors trois prédicats qu’on unifiera: un prédicat propose les nombres absents de la ligne, un autre les nombre absents de la colonne et un dernier les nombres absents du carré. Ainsi, pour obtenir une valeur valide pour la case, on unifie les trois.

Notons dès maintenant qu’ajouter une valeur valide ne garantit pas que cela mènera à une solution. En effet, il existe des grilles valides mais sans solution.

Génération d’une ligne valide

La seconde étape est de générer une ligne valide, c’est-à-dire une ligne remplie de valeurs valides. Elles sont donc différentes de chacune des autres valeurs de leurs colonnes et carrés respectifs. Cette génération se fait de manière récursive: pour la position I, on récupère la liste ayant les indices supérieurs à I remplis avec de valeurs valides. On génère ensuite une valeur valide pour la position I dans cette liste ayant été obtenue récursivement. En faisant un appel avec l’indice 1, on obtient donc une liste résultat contenant uniquement des valeurs uniques. Dans cette génération on ne supprime évidemment pas les valeurs déjà présentes dans la liste.

Génération d’une solution

L’étape finale est un peu semblable à l’étape précédente mais à une échelle supérieure. On utilise un prédicat récursif: pour la ligne I, on récupère récursivement un board rempli avec des lignes valides aux indices supérieurs à I. On insère donc une ligne valide à la position I.La ligne I devra donc être valide par rapport au tableau de départ complété par les valeurs valides générées précédemment. Si pour une ligne I, il n’existe pas de ligne valide, le programme va faire un retour arrière et changer les lignes précédemment générées.

Génération avec gradient de difficultés

Tout d’abord on utilise produit une grille valide remplie avec une dizaine de valeurs aléatoires. ensuite on utilise notre algorithme de résolution pour obtenir une solution de la grille à laquelle on va supprimer des cellules pour que l’utilisateur puisse jouer. On a rempli partiellement la grille de manière aléatoire pour obtenir à chaque partie de nouvelles grilles. En effet, le résolveur résoudra toujours de la même manière une grille vide donc on aura un manque de diversité dans les grilles produites. La difficulté d’un sudoku provient de trois facteurs majeurs;

• le nombre de cellules initiales données au joueur

• le choix de l’algorithme de “digging hole” (c’est-à-dire de parcours de la grille et de vérifications des cellules candidates pour supprimer)
• l’application des propagations équivalentes telles que les rotations, les permutations des colonnes (1 par 1 ou 3 par 3).

Digging hole

On distingue dès lors quatre type de séquences d’établissement des digging holes;

• Left to Right Then To Bottom
• Wandering along S
• Jumping One Cell
• Randomizing globally

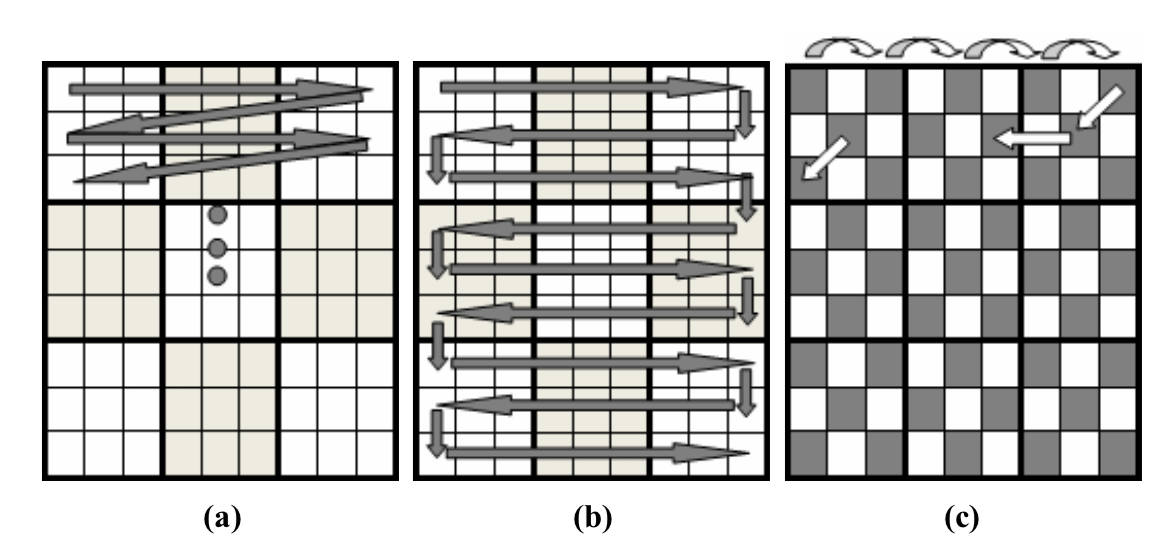
Dans notre algorithme, nous avons implémenter, par faute de temps, que deux types de séquences. Pour les difficultés faciles et extremement faciles, nous utilisons une séquence Randomized Globally, c’est-à-dire que l’on génère aléatoirement un couple (I,J) puis on vérifie si la suppression de cette cellule maintient l’unicité de la solution. Pour les difficultés moyennes et difficiles, nous obtenons la grille en supprimant les cellules obtenues par Jumping One Cell (on génère d’abord un couple puis on le fait déplacer selon des directions aléatoires). Avec cette algorithme de déplacement de la cellule à supprimer, il est possible que l’on rencontre un échec où toutes les cellules adjacentes sont déjà supprimées. Dans ce cas, il va falloir relancer la suppression sur une cellule aléatoire.

Propagation

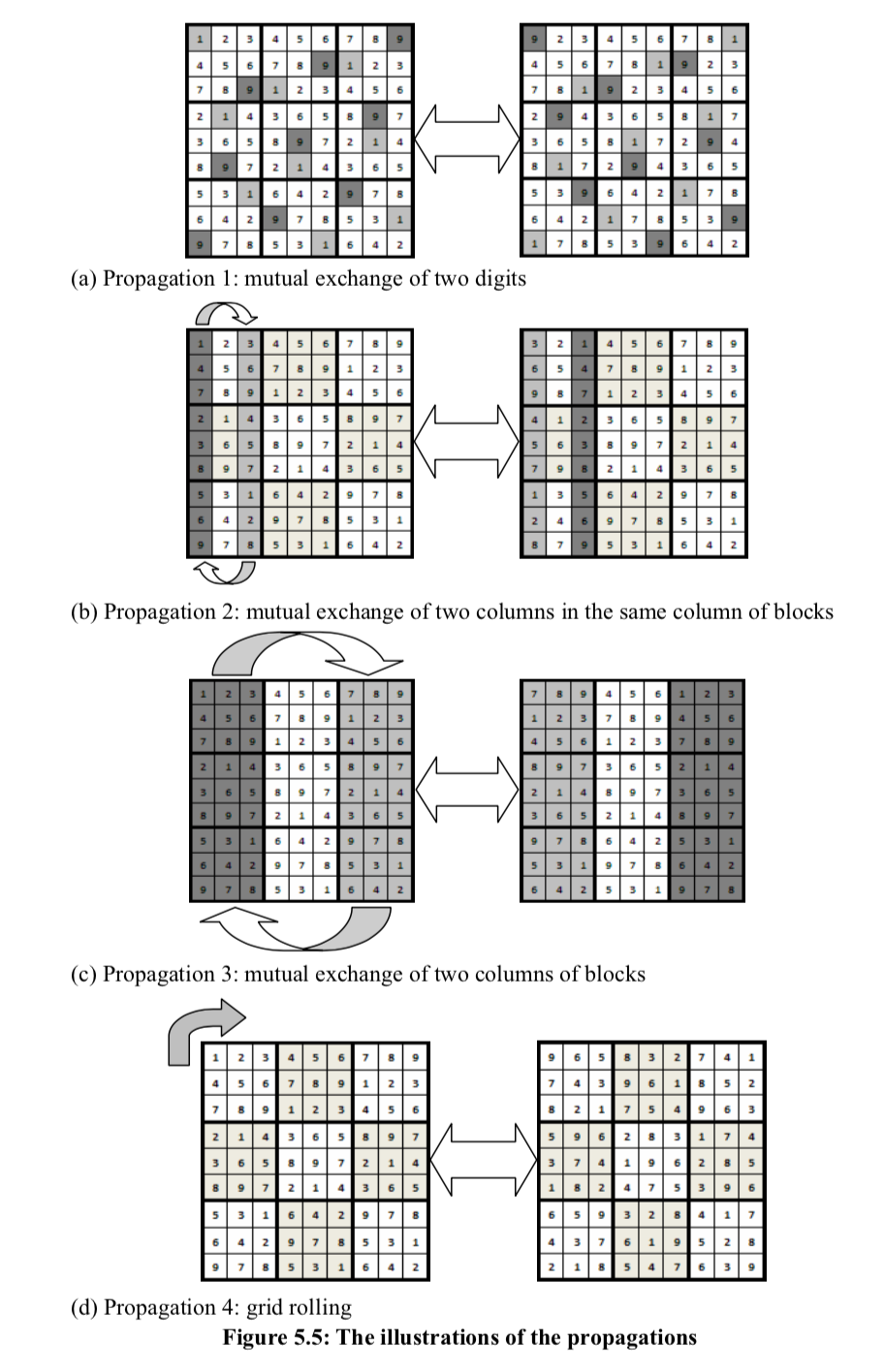
Pour les sudoku de difficultés importantes, il est nécessaire que les symétries, ou les motifs ne soient pas visibles au joueur. Dès lors, on doit appliquer des algorithmes qui permettent, à partir d’une grille valide remplie, d’en générer une autre sans trop de calculs complémentaires. Ces algorithmes, nommés des algorithmes de propagation telles que la rotation de la matrice, l’échange des colonnes permettent masquer ses motifs, tout en préservant l’ensemble des propriétés d’un sudoku valide. Nous avons implémentés ces permutations pour les jeux “medium” et “hard”.

Améliorations possibles

L’interface

D’une part, jouer dans la console n’est pas très pratique, particulièrement pour le sudoku. Il serait donc intéressant de générer une fenêtre. D’autre part, nous n’avons pas réussi à créer une boucle de génération de solutions illimitée. En effet, notre boucle aura un nombre précis d’itérations. Nous n’avons pas réussi à faire une boucle qui s’arrête soit si le joueur le souhaite, soit si il n’y a plus de solutions. De plus, on pourrait faire un mode qui guide un joueur débutant dans la résolution d’une première grille (une sorte de tutoriel).

La difficulté

Nous avons essayé de nous approprier rapidement l’article mais on se rend bien compte qu’il existe des cas où là génération de grilles ne fournit pas forcément une grille du niveau souhaité (ceci est surtout vrai pour les grilles de difficultés moyenne et difficile). On pourrait donc relire cette article et retravailler notre code. De plus, avec un peu plus de temps, on pourrait le confronter avec d’autres articles de la littérature traitant du sudoku (de manière académique).