🇫🇷 Pokemon victory prediction

Ce travail a été fait avec Alix CANDUSSO et Chen GONG dans le cadre de l’UV SY09.

Issu d’une franchise de jeu vidéo japonaise, un pokémon est une créature qui, une fois capturée par un dresseur, peut-être envoyé pour affronter les pokémon d’un autre dresseur. Régi par un ensemble de règles bien définies, la complexité des combats qui en dérive et les modèles qui les prédisent constituent l’intérêt de cette étude.

Analyse exploratoire

Cette collection, provenant de Kaggle, est constituée de trois jeu de données différents;

Caractéristiques d’un pokémon

Ce jeu de données présente les caractéristiques de 800 pokémon extraites directement du code objet du jeu. Chaque pokémon, identifié de manière unique par un nom ou un entier, se caractérise par un booléen qui indique s’il est légendaire ainsi que par sa génération (“version” à partir de laquelle le pokémon a été ajouté). Un pokémon est aussi caractérisé par ses statistiques;

speed: détermine s’il prend l’initiative lors d’un combat
hp: nombre de point de dommages qu’il peut subir avant d’être éliminé
attack: puissance de ses attaques physiques
defense: résistance aux attaques physiques
sp. attack: puissance des attaques “magiques” (le pokemon ne touche physiquement pas son adversaire mais inflige tout de même des dégâts)
sp. defense: résistance aux attaques spéciales

Normalement, les statistiques d’un pokémon sont basées sur des statistiques de base augmentent lorsque le pokémon monte en niveau, mais cette dimension n’est pas considérée dans ce jeu de données. De plus, chaque pokémon appartient à un ou deux types (e.g. Feu, Eau, Acier, Électricité, Vol…) qui indique quelles capacités peuvent être apprises et ses forces/faiblesses par rapport à des pokémon d’autres types (e.g. les pokemon de type Feu sont plus vulnérables aux attaques de type Eau, mais plus résistants aux attaques de type Plante).

Combats

Ce tableau présente les codes des belligérants de 50001 duels et le vainqueur. Ces triplets synthétiques sont générés par un algorithme qui simplifie certains aspects du jeu notamment les capacités. En réalité, un combat se déroule selon les règles suivantes:

Le pokémon présent dans la première colonne dispose de l’initiative pour le premier tour.
À chaque tour, chaque pokémon choisit et utilise une de ses quatre capacités (une attaque physique ou spéciale, une attaque de modification de statistiques, etc) jusqu’à ce que les points de vie de l’un des deux tombe à 0 et la victoire est alors accordée à l’autre.

Afin d’alléger la notation, notons dorénavant $\Omega$ (l’ensemble des pokémon) et donc $\Omega^2$ (l’ensemble des statistiques de deux pokémon qui s’affrontent en duel).

En interpolant à partir des données sur les combats, on peut émettre l’hypothèse que le résultat d’un combat entre deux pokémons est déterministe car:

Il n’y a pas de combats où un pokémon affronte l’exact même pokémon. Si ce cas de figure existe, les deux belligérants auraient exactement les mêmes statistiques de combats et le résultat devrait donc être soit décidé de manière aléatoire soit une égalité.
Il n’y a pas deux combats entre $p_1$ et $p_2$ où dans l’un $p_1$ attaque en premier et dans l’autre il attaque en deuxième.
Chaque combat a un gagnant unique.

Il est donc possible de construire un classifieur binaire pour prédire le résultat d’un combat où $True$ correspond à la victoire du premier pokémon qui attaque et $False$ sinon. Néanmoins, seulement $14.409%$ des combinaisons de paires possibles de pokémon sont représentées donc notre modèle sera entraîné sur une partie relativement petite de l’ensemble $\Omega^2$. Un échantillon de test accompagne aussi la table des combats. Tout de même, celui-ci est inutile pour vérifier la validité du modèle car il ne présente pas le code du vainqueur.

Problématique

Le but ce cette étude est donc d’appliquer un large éventail d’algorithmes d’apprentissage supervisés et non supervisés afin de construire un modèle, qui, prend en entrée deux pokémon et prédit le gagnant.

Enrichissement du jeu de données

Introduction d’une hiérarchie

Un pokémon dispose parfois d’une chaîne d’évolution (e.g. Salamèche $\rightarrow$ Reptincel $\rightarrow$ Dracaufeu), les pokémon en fin de chaîne étant en général plus puissants que ceux en début. Afin de tester si cette catégorisation hiérarchique contribue à la améliorer la classification, nous avons introduit le stage d’évolution d’un pokemon (0 étant l’état en début de chaîne d’évolution qui incrémente de 1 jusqu’à ce qu’on atteint un pokémon en fin de chaîne) grâce à PokeAPI.

Ajout d’une métrique

Afin de combiner le jeu de données des pokémon et des combats, il est possible de comprimer le tableau de combats en une seule métrique, le taux de victoire avec la formule:

$$win\_rate(p_i) = \frac{nombre\_de\_victoires(p_i)}{nombre\_de\_combats(p_i)}$$

Matrice des corrélations des caractéristiques des pokémon

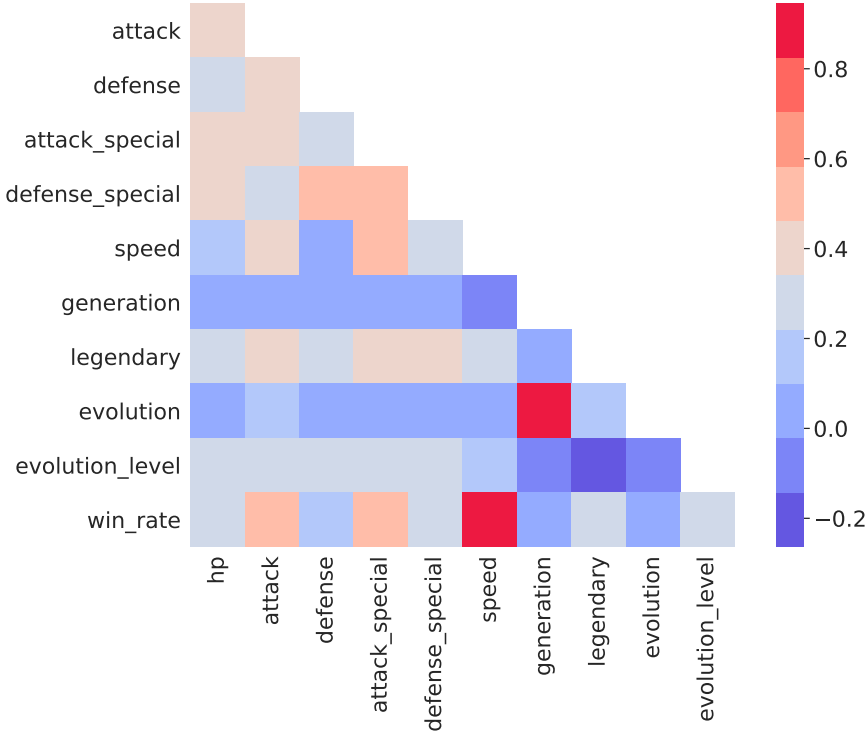
La matrice de corrélation issue du jeu de donnée enrichi démontre une corrélation forte entre la vitesse d’un pokémon et son taux de victoire ainsi que le niveau d’évolution et la génération. La deuxième relation s’explique par l’introduction des chaînes d’évolutions plus longues au fur et à mesure de la parution de nouveaux jeux Pokémon (e.g. évolutions méga, X ou Y).

Il est tout de même surprenant que les attributs de défenses (hp, defense, sp. defense) affectent très peu le taux de victoire du pokémon. Au contraire, les attributs offensifs (speed, attack, sp. attack) sont plus fortement corrélés à la probabilité de gagner un duel.

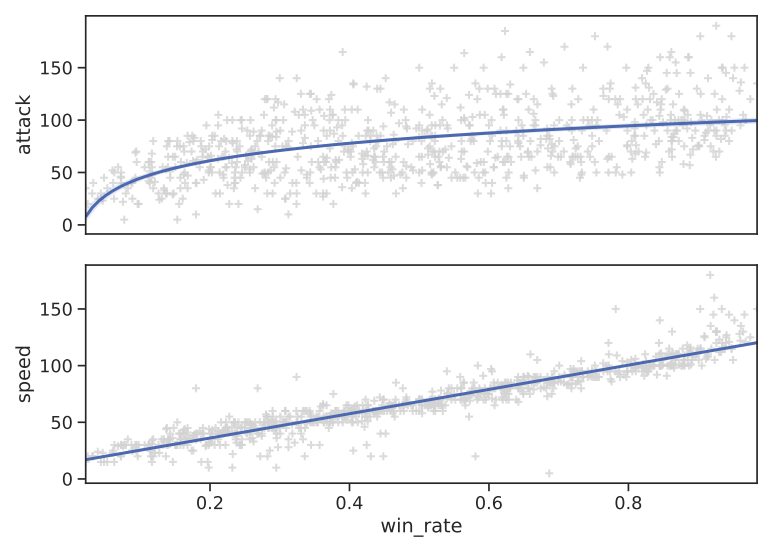
Regréssion des attributs les plus fortement corrélés au taux de victoire

De même, le jeu de données des combats peut être enrichi en ajoutant les caractéristiques de chaque participants. Tout de même, le tableau individu-variable de taille importante ($50001$ lignes et $21$ colonnes) qui en résulte ralentit l’entraînement des algorithmes et augmente la quantité de ressource consommée. Il sera donc nécessaire de réduire ses dimensions via des algorithmes linéaires (PCA) linéaire ou en agrégeant les attributs en des métriques plus conséquentes.

Au lieu de considérer les attributs attaque/attaque spéciale et défense/défense spéciale, il est aussi possible d’additionner les deux statistiques pour en former une statistique attaque et défense plus générale (ce jeu de donnée s’appellera désormais reduced_diff).

Impact des types

Afin d’étudier l’impact des mécanismes de faiblesse par rapport aux types des deux combattants sur l’issue du duel, deux attributs ont été ajoutés, le multiplicateur de puissance d’attaque de chacun des pokémon. Ces dernières réduisent quatre valeurs qualitatives (catégorie) en deux valeurs quantitatives grâce à la formule:

$$\tau_{type_1(p_1),type_1(p_2)} \times \tau_{type_1(p_1),type_2(p_2)}$$

$$\tau_{type_2(p_1),type_1(p_2)} \times \tau_{type_2(p_1),type_2(p_2))}$$

Avec $\tau$ la matrice des multiplicateurs de la puissance d’attaque de la VIIème génération, avec $\tau_{t_1,t_2} \in \mathbb{R}^+$ le multiplicateur d’attaquant de type $t_1$ par rapport à un défendant de type $t_2$. Afin d’obtenir le multiplicateur dans le sens inverse, il suffit de prendre $mult(p_2, p_1)$.

	victoire du 1er pokémon	victoire du 2nd pokémon
mult(p1,p2)> mult(p2,p1)	0.51346	0.48654
mult(p1,p2)=mult(p2,p1)	0.481212	0.518788
mult(p1,p2)< mult(p2,p1)	0.415805	0.584195
total	0.47202	0.52798

La matrice de contingence relative entre ses multiplicateurs et l’issue du combat, révèle une inclinaison positive vers la victoire du $2^{nd}$ pokémon ainsi qu’une absence de corrélation claire entre l’avantage que confère le type et la victoire.

Réduction des dimensions

Analyse en composantes principales

Pour le jeu de données des combats, la colonne vainqueur pose problème puisqu’elle est logiquement fortement corrélée à first_pokemon et second_pokemon et difficilement manipulable. La conversion de l’attribut vainqueur en un booléen qui représente si le vainqueur correspond bien au premier pokémon, donne un domaine $\Omega^2 \times {True, False}$ plus facile à manipuler.

Dès lors, l’application d’une ACP s’avère utile à cause du fléau de la dimension en permettant de projeter l’espace précédente dans un espace $\mathbb{R}^n$ avec $n$ le nombre d’axes factoriels. Les contributions relatives des axes d’une ACP avec l’ensemble du tableau révèlent un coude au niveau du deuxième axe factoriel. Néanmoins, même si les premiers et deuxièmes axes expliquent $91.36%$ de l’inertie totale, l’introduction d’un troisième axe donne une structure nettement séparée entre les classes au lieu des classes confondues (axe1-axe3).

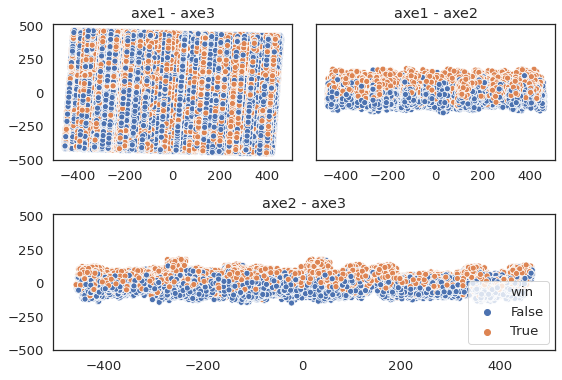
ACP des combats à trois axes factoriels.

Matrice de distance intermédiaire

Il est possible de réduire l’espace sans une ACP en soustrayant les statistiques des combattants. Certaines des différences obtenues corrèlent fortement à l’issue du duel. La combinaison de ces différences peut donc révéler une fonction de distance $d:\Omega^2 \mapsto \mathbb{R}$ et une fonction de régression $r: \mathbb{R} \mapsto {True, False}$ qui donne en combinaison la classification voulue : $clf = r \circ d$.

Tout de même, la table des combats contient des variables qui ne permet pas à l’évaluation. Les variables qualitatives comme le type des pokémon sont transformées par la formule des types. Les attributs booléennes peuvent être convertis en $0(False), 1(True)$ puis une soustrait. Néanmoins, puisque cette conversion nuît à l’interprétabilité du modèle, les variables booléennes sont alors éliminées.

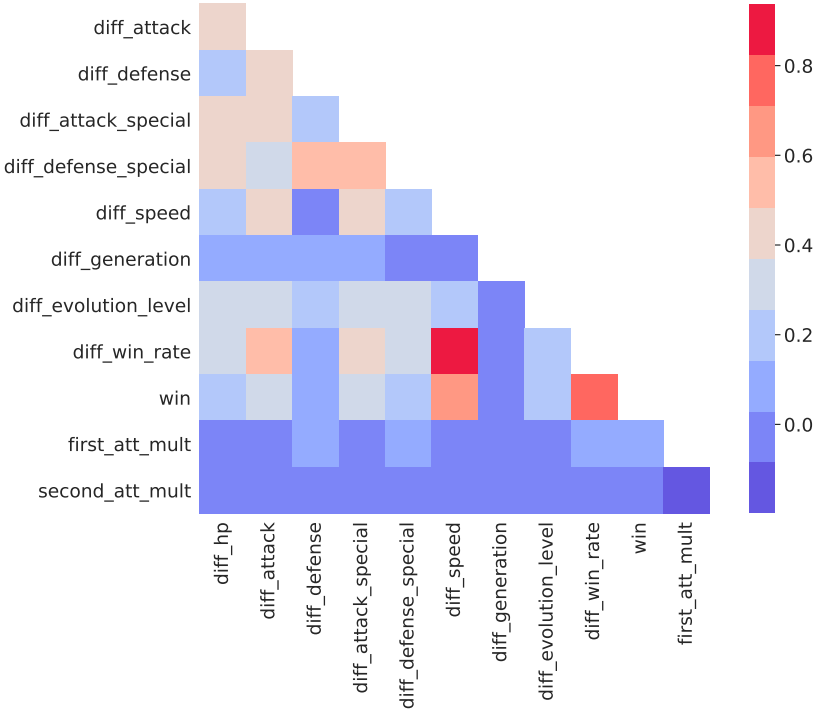
Pour les autres statistiques de combats et les taux de victoires, une différence absolue est utilisée afin de respecter la symétrie de la distance. Il est possible d’utiliser la différence exacte de la différence des taux de victoires mais celle-ci nécessite que l’ensemble des anciens adversaires soient relativement conséquentes. Or, la matrice des combats est creuse ($14%$ de remplissage).

$$\frac{|V(p_1) \cap Adv(p_1,p_2)| - |V(p_2)\cap Adv(p_1,p_2)|}{|Adv(p_1,p_2)|}$$

$$V(p_1) = vaincus, par, p_1$$

$$Adv(p_1) = adversaires, de, p_1$$

$$Adv(p_1,p_2) = Adv(p_1) \cap Adv(p_2)$$

De plus, il est possible de réduire d’autant plus la dimension en effectuant une ACP sur ces différences. La méthode du coude révèle que 6 axes factoriels expliquent la majorité de la variance expliquée.

K Plus Proches Voisins (KNN)

Principe

L’algorithme des KNN est une méthode de classification supervisée qui ne nécessite pas d’apprentissage. Lorsque l’on souhaite classer une nouvelle donnée, on relève les K plus proches voisins (en termes d’attributs) parmi le jeu de données existant et on classe cette nouvelle donnée dans la classe prédominante parmi les K plus proches voisins qui l’entourent.

Application

En faisant varier le nombre de dimensions de la PCA, on observe que la performance de l’algorithme sur le dataset des différences est optimale à 6 axes factoriels. De plus, la réduction de la dimension semble diminuer le nombre de voisins à partir duquel les KNNs convergent vers la qualité de prédiction optimale.

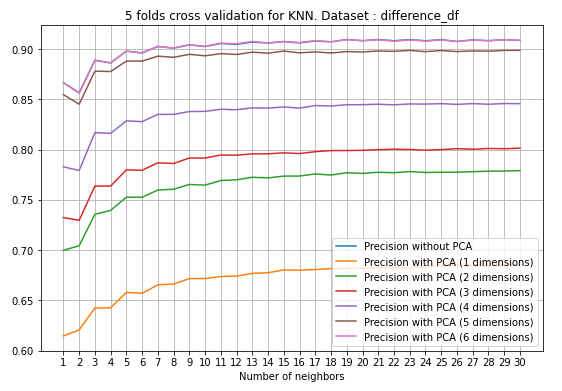
Validation croisée à 5 coupes des KNN en fonction du nombre K de voisins et de la dimension de l'ACP

Au-delà d’un certain seuil de voisins, la croissance en terme de qualité de prédiction est négligeable et ne justifie pas le coût algorithmique supplémentaire. Pour notre jeu de données, ce seuil se trouve aux alentours de 20 voisins et donne un accuracy_score de $91%$. De même, l’application sur reduced_diff donne les mêmes observations mais avec une précision légèrement améliorée.

Par défaut, l’implémentation KNN de sklearn utilise une distance euclidienne pour trouver les voisins les plus proches et chaque individu est pondéré de manière uniforme. Le choix de la distance détermine en pratique la forme du volume de dimension $N$ qui délimite les frontières d’un point;

euclidien ($\sqrt{\Sigma(x - y)^2}$) : sphère de $N$ dimensions.
manhattan ($\Sigma(|x - y|)$) : cube de $N$ dimensions
chebyshev ($max(|x - y|)$) : cube de $N$ dimensions où la longueur correspond à la distance maximale d’un attribut entre deux individus donnés.

La distance de manhattan aurait donc tendance de considérer plus d’individus comme voisins que par rapport aux autres. En appliquant sur le jeu de données, on observe que l’utilisation de cette manhattan donne le meilleur estimateur parmi les autres distances. Une piste d’amélioration serait alors d’étudier l’effet des distances qui engendrent des volumes plus important (par exemple les distances de minkowski avec $p \in ]0,1[$).

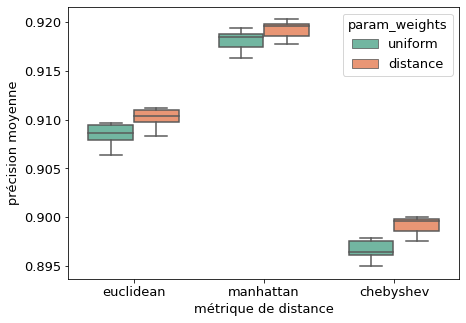
Qualité du modèle KNN selon la distance et la pondération des individus après validation croisée à 5 coupes

De même, la qualité du modèle issu de la distance de manhattan suggère qu’il n’est pas sur-apprenti (l’inclusion de plus de points l’améliore). On peut donc renforcer l’effet de la distance dans l’algorithme en donnant chaque individu un poids qui correspond à l’inverse de sa distance à l’élément à classifier (option distance sur sklearn). Cette modification améliore un tout petit peu la qualité et confirme l’hypothèse précédente.

Support Vector Machine (SVM)

Principe

Les machines à vecteurs de support (Support Vector Machine) ont pour but de séparer les données en classes à l’aide d’une frontière aussi simple que possible, de telle façon que la distance entre les différents groupes de données et la frontière qui les sépare soit maximale. Cette distance est aussi appelée marge et les données les plus proches de la frontière sont appelées les vecteurs de support.

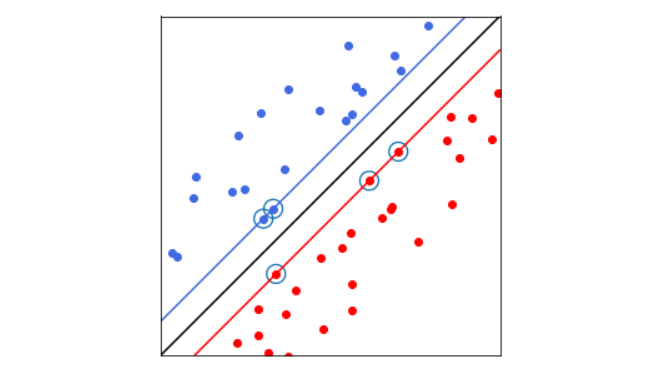
Illustration d'un SVM avec la frontière (droite noire), les vecteurs de support (points entourés) et les marge (droites bleue et rouge)

Pour un problème de classification binaire, la frontière de décision est un hyperplan défini par; $$h(x)=w^{T}x+b = 0$$

$x$ les données d’entrée de dimension $N$, $w$ le vecteur des poids et $b$ la distance entre l’hyperplan et l’origine. Trouver l’hyperplan de marge maximale revient donc à:

$$\frac {1}{2}||w||^{2}, \quad \quad l_{k}(w^{T}x_{k}+w_{0})\geq 1$$

avec ${\displaystyle l_{k}}$ le label du vecteur $x_k$, ${\displaystyle l_{k}} \subset {\displaystyle {-1,1}}$. Ceci peut se résoudre par la méthode classique des multiplicateurs de Lagrange, avec le lagrangien:

$$L(w,b,\alpha)=\frac {1}{2}||w||^{2}-\sum_{k=1}^{p}\alpha_{k}(l_{k}(w^{T}x_{k}+b)-1)$$

Le lagrangien doit être minimisé par rapport à w et b, et maximisé par rapport à $\alpha$. Après avoir résolu $\alpha$, on trouve w et b pour obtenir le modèle:

$$h(x)=\sum_{k=1}^{p}\alpha_{k}^{*}l_{k}(x\cdot x_{k})+b$$

Pour les problèmes séparables non linéaires dans l’espace d’origine, l’échantillon peut être mappé de l’espace d’origine vers un espace d’entités de dimension supérieure, de sorte que l’échantillon est séparable linéairement dans cet espace d’entités grâce à une fonction de noyau (kernel).

Application

La clé de l’application d’une SVM réside dans la sélection des fonctions du noyau. Les fonctions de noyau doivent correspondre à un produit scalaire et les plus couramment utilisées comprennent: \begin{itemize}

noyau linéaire : sans changement d’espace, on se ramène à une classification linéaire.
noyau polynomial : $K(u,v) = (coef0 + \langle u, v\rangle)^d$ avec $d$ le degré du polynôme; un degré de $1$ revient à faire un noyau linéaire et à des degrés trop grand, le modèle risque de sur-apprendre.
fonction de base radiale : $K(u,v) = exp(-\gamma \times\Vert u, v\Vert)$. Cette fonction donne en générale des bons résultats pour des séparations non linéaires.
noyau sigmoïde: $K(u,v) = tanh(\gamma \times\Vert u, v\Vert + coef0)$

La Figure suivante permet de visualiser la différence des marges et de la frontière entre les noyaux. Tout de même, il n’est pas possible de visualiser les données à dimension $> 2$ et donc d’estimer quel kernel est le mieux adapté.

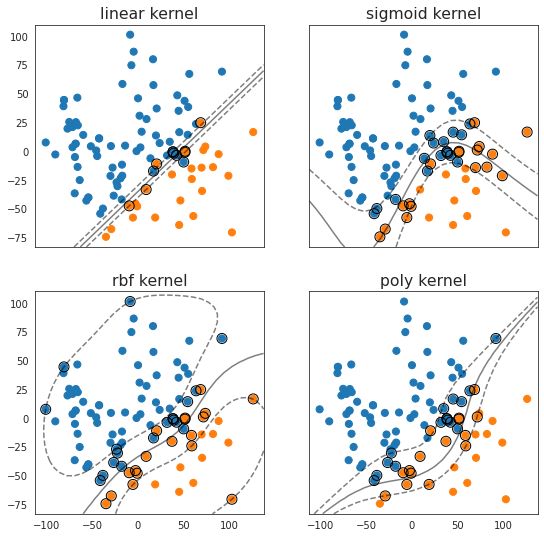
Comparaison de la frontière des différentes kernel sur une PCA à deux dimensions des différences des pokémons

En testant tout les kernels de base dans la librairie de sklearn, l’utilisation d’un kernel RBF donne en moyenne un meilleur estimateur ainsi que le temps d’entraînement le plus rapide pour notre jeu de données.

kernel	accuracy score moyenne (cv 5)	temps d’entraînement moyen (en s)
linear	0.899007	3981
poly	0.864955	20.998
sigmoid	0.7146	27.892
rbf	0.9273	11.822

Le kernel RBF peut être régularisé grâce à deux paramètres; $C$ et $\gamma$. Où $C$ est le coefficient de pénalité, qui correspond à la tolérance aux erreurs; un $C$ grand pousse le modèle à apprendre parfaitement tandis qu’un $C$ petit cherche à lisser la frontière de décision. Le gamma lui, détermine l’importance de chaque individus d’entraînement; plus le $\gamma$ est petit, plus les vecteurs de support sont nombreux, ce qui réduit la vitesse d’entraînement et de prédiction.

En faisant une recherche aléatoire sur les deux espaces, on observe qu’un coefficient de pénalité faible et un gamma faible améliore le résultat.

Arbre de décision

Principe

Ce modèle cherche à construire une partition de l’espace $\Omega^2$ dans laquelle l’issue des combats dans chaque sous-ensemble est homogène grâce à un arbre binaire.

A partir de la racine qui représente l’ensemble de départ, 0 à 2 noeuds sont ajoutés. Chaque noeud représente une division, c’est-à-dire une condition sur un attribut ou une combinaison linéaire d’attributs coupant l’ensemble en deux sous-ensemble. Cette procédure est répétée pour chaque sous-ensemble récursivement jusqu’à l’obtention des partitions homogènes au sens de la variable à prédire. Afin d’avoir une séparation optimale à chaque étape, l’algorithme cherche la division qui optimise le critère d’impureté par une recherche à force brute (itération sur l’ensemble des seuils possibles).

Régularisation

La capacité de généralisation d’un arbre par rapport à son ensemble d’apprentissage dépend fortement de sa profondeur. La définition d’une profondeur maximale ou d’un nombre de noeuds maximal permettent de limiter la croissance manuellement à condition qu’une division de l’espace soit trouvée lors des visualisations. Sinon, un \textbf{seuil minimal de décroissance d’un critère} entre chaque développement de l’arbre peut être utilisé pour limiter la croissance en complexité sans perdre la précision du modèle.

Application

L’analyse de l’impact du paramètre de croissance minimale d’impureté sur la qualité du modèle de prédiction de la victoire à partir des différences montre qu’une croissance trop ralenti ($c_{min}>0.4$) entraîne un sous-apprentissage et une croissance non contrôlée un sur-apprentissage.

De plus, l’optimum global obtenu à $c_{min} = 0.15$ est commun entre les deux critères de pureté et produit deux arbres équivalents de profondeur 2. La bonne qualité de la prédiction ($94.5%$ de bonne prédiction à l’issu d’une validation croisée à 5 coupes) s’accompagne aussi de l’interprétabilité car le modèle revient à deux conditions sur la différence de vitesse et d’attaque entre les deux pokémon.

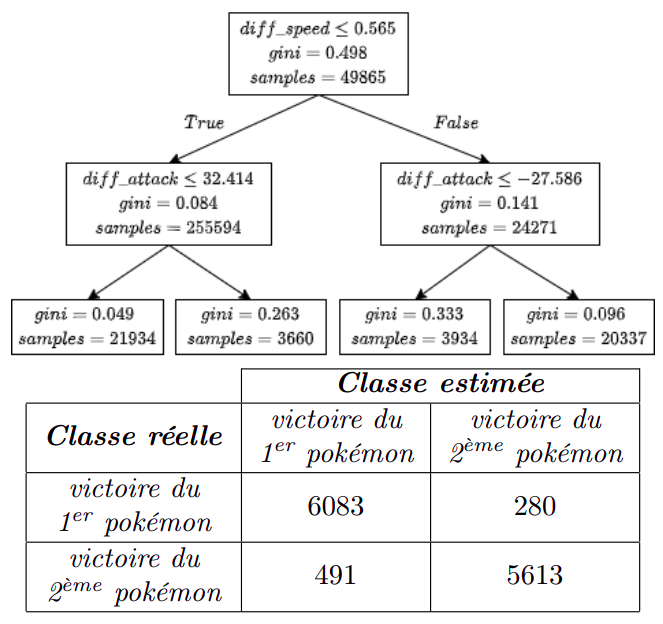
Arbres de décision de la différences des statistiques des combats et matrice de confusion sur l'échantillon de test de 12466 individus

La matrice de confusion révèle tout de même qu’une grande partie des erreurs de classification commises s’explique par une sur-estimation de la capacité du premier pokémon. Ceci peut provenir d’un léger biais pour la perte du premier pokémon que nous allons tenter de prendre en compte dans la partie Forêt Aléatoire.

De plus, l’arbre de décision produit un estimateur de variance élevée; les séparations sont optimisées localement et souvent sous-optimales, et donc chaque changement léger dans les données produit des arbres complètement différent.

Forêt aléatoire

Principe

La forêt aléatoire permet de régler le problème de la variance des arbres de décision en regroupant plusieurs arbres en un modèle plus complexe.

L’algorithme consiste d’abord à créer $N$ réplications des données initiales $D$ par tirages avec remise, nommés les échantillons de bootstrap $D^*_b$. On entraîne alors les arbres de décisions $A_b$ avec les données d’entraînements $D^*_b$ par un algorithme CART légèrement modifié; le découpage choisi correspond à la séparation qui optimise le critère d’impureté sur un ensemble d’attributs tiré aléatoirement parmi les attributs. Finalement, le classement d’un individu se fait par vote majoritaire des arbres.

En moyennant les prédictions d’un groupe d’arbre, on réduit la variance des arbres individuelles et en construisant des arbres sur des échantillons différentes et des attributs différents, on diminue le biais du modèle.

Application

La régularisation d’une forêt est similaire à celle d’un arbre mise à part le paramètre du nombre d’arbres qui constituent la forêt. De plus, afin de réduire l’effet du biais négative des données, on peut attribuer d’un poids à chaque classe pondère la proportion des classes dans le calcul des critères d’impureté:

$$C_l(p) = p_l^{-}(1 - p_l^{-}) + p_l^{+}(1 - p_l^{+})$$

$$avec\ p_l^{-} = \frac{n_l^{-} \times w^{-}}{n_l}$$

Avec $C$ le critère d’impureté, $p^{+}l$ les proportions à un noeud $l$ des différentes classes pour les individus de l’arbre inférieur au seuil et $\omega{+}$ le poids associé à la classe Victoire du premier pokémon. Dans ce problème binaire, en augmentant le poids d’une modalité, on augmente son influence sur la croissance de l’arbre et on réduit en même temps la modalité inverse.

En associant un poids plus important à la défaite, la qualité des prédictions des arbres binaires et des forêts aléatoires s’améliorent de manière négligeable. La fluctuation de la qualité des prédictions par rapport aux poids des classes pour l’arbre de décision peut s’expliquer par la variance importante du modèle et ne peut donc pas être prise en compte. Même en utilisant l’option balanced pour les poids des classes sur sklearn et en augmentant le nombre de plis de la validation, aucune différence statistique pertinente est observable. L’observation que nous avons fait au niveau du biais des données n’affecte donc pas le classifieur.

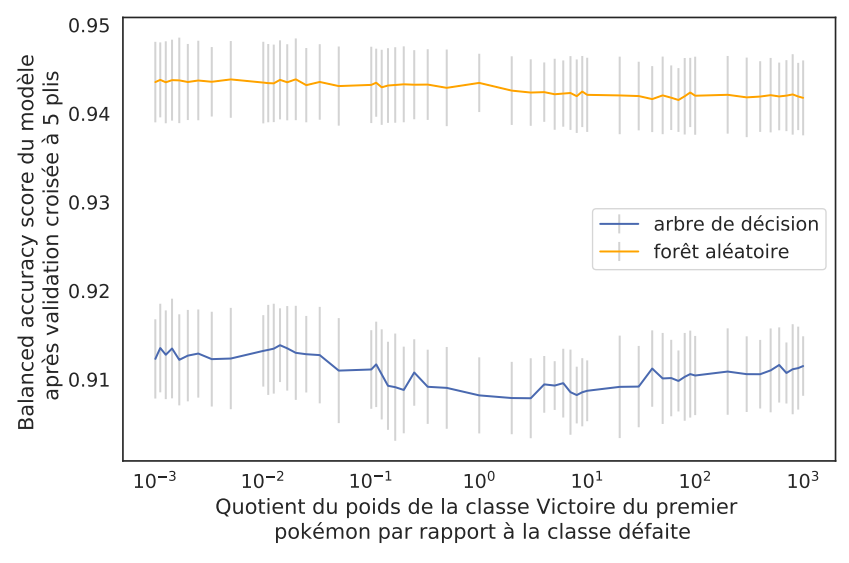
Qualité du modèle de prédiction des taux de victoire par rapport aux poids attribués à chaque classe (sans optimisation d'autres hyper-paramètres)

Adaptative Boosting

Principe

Le boosting est une méthode qui consiste à construire séquentiellement une suite de modèles simples pour constituer un modèle plus puissant.

Pour un problème de classification binaire d’une variable $y$, l’algorithme Adaboost considère que les individus sont tous initialement uniformément pondérés. A l’itération $i$, un nouveau modèle $M^i$ est construit avec le modèle de base sur l’échantillon d’entraînement avec le poids courant des individus. Son taux d’erreur $\varepsilon^i$ de classification est alors calculé puis le poids $\alpha^i$ ainsi que la pondération des individus $\omega_j$ qui sera ensuite normalisée. L’algorithme converge lorsque le nombre de modèles est satisfait ou lorsque l’erreur est plus petite qu’un seuil donné.

$$\varepsilon^i = \frac{\sum_{j=1}^n\omega_j\unicode{x1D7D9}(y_j \neq M^i(j))}{\sum_{j=1}^n\omega_j}$$

$$\alpha^i = log\left(\frac{1 - \varepsilon^i}{\varepsilon^i}\right)$$

$$\omega_j^{i+1} = \omega_j^{i} \times exp(\alpha^i \times \unicode{x1D7D9}(y_j \neq M^i(j)))$$

La mise à jour de la pondération des individus attribue un poids plus important aux individus mal classifiés, ce qui incite le modèle de boosting sur les itérations suivantes à corriger les zones problématiques en terme de classification. Cet avantage est à double tranchant puisqu’il rend le modèle plus sensible aux données bruitées ainsi qu’à une mauvaise classification.

En générale, Adaboost fonctionne mieux avec des modèles de base simples avec des puissances de prédiction faible comme les arbres de décision.

Application

L’application d’Adaboost sur l’arbre de décision donne un résultat similaire à un arbre simple. Ce s’explique par la complexité de l’arbre optimal initial (de profondeur 5) ainsi que la présence des résultats inattendus de certains combats (victoire d’un pokémon défavorisé à l’égard des statistiques de combats) auxquelles le modèle est plus sensible.

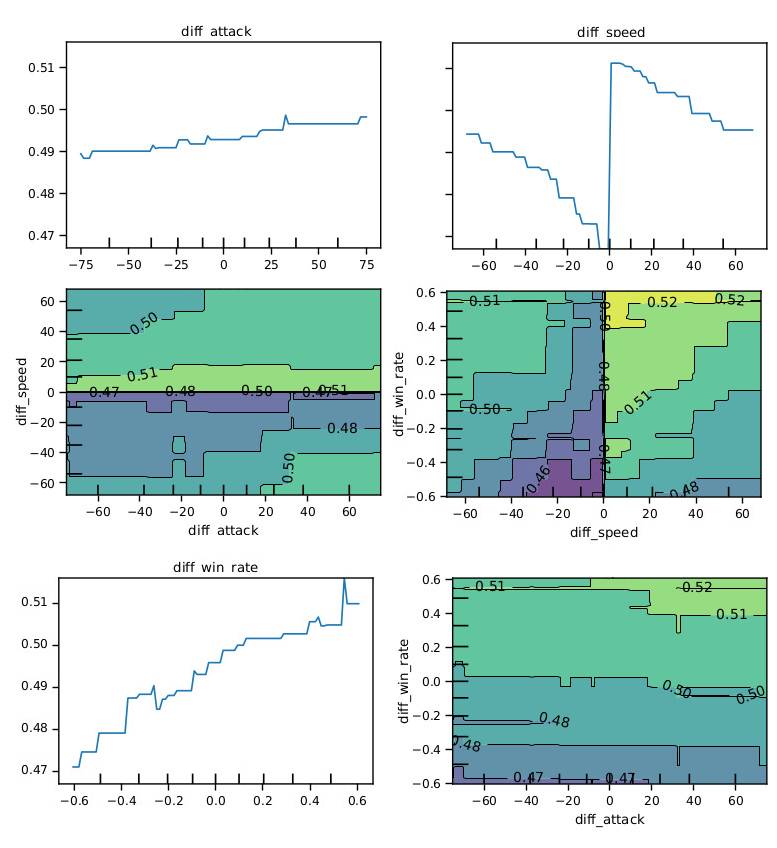
Graphique de dépendance partielle des variables les plus importantes du modèle Adaboost de prédiction des combats

Le graphique de dépendance (représentation qui montre l’influence d’une ou de plusieurs variables marginales sur la prédiction. Pour un problème de classification binaire, toute zone de probabilité $>0.5$ correspond à un $True$.) montre une rupture des frontières de décision claire qui se produit au niveau de diff_speed $= 0$. La dépendance partielle de la différence de vitesse va contre l’intuition que la différence de vitesse influence linéairement la probabilité de victoire du pokémon avantagé.

La forme inattendue ($1/x$) que prend la dépendance partielle des différence de vitesse peut s’expliquer par la dominance des différences des taux de victoires dans le modèle. L’inclusion de cette variable bruitée affaiblit fortement le modèle. Sa suppression engendre alors une amélioration visible du taux de prédiction correcte de $0.909$ à $0.940$ et une correction de l’évolution de la dépendance partielle.

Conclusion

Évaluation des performances

Afin de comparer les performances entre différentes familles d’algorithmes, la procédure commune suivante a été suivie:

Le jeu de données est divisé en un échantillon d’entraînement et de test ($33%$ des données) grâce à GridSearchCV.
L’estimateur de performance choisie est l’accuracy_score qui calcule la correspondance exacte de la prédiction et de la classe réelle par la formule: $$\texttt{accuracy}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} \unicode{x1D7D9}(\hat{y}_i = y_i)$$ Cet indicateur correspond bien à notre cas d’usage puisqu’il s’agit d’un problème de classification binaire où le résultat d’un combat est déterministe.
Le critère de qualité est alors calculé par validation croisée à cinq coupes afin de réduire le biais et optimisé sur l’espace d’hyper-paramètre correspondant.

Modèles	Accuracy score
KNN	0.92
SVM	0.9273
Arbre de décision	0.945
Forêt aléatoire	0.949
AdaBoost d’arbre	0.940

Même avec une évaluation pessimiste de la qualité, les modèles construits peuvent tous répondre adéquatement à notre problématique.

Afin de minimiser le temps d’entraînement, d’optimiser la qualité du modèle et de maintenir l’interprétabilité, l’arbre de décision correspond au choix optimal pour notre jeu de données synthétiques. On peut alors émettre l’hypothèse suivante sur la génération des données : la victoire est générée selon deux conditions sur la différence de vitesse et d’attaque entre les deux pokémons puis du bruit aléatoire introduit pour complexifier la classification.

Conclusions et futurs travaux

Ce projet nous a permis d’appliquer et de comprendre les algorithmes de classification vus en cours sur un jeu de données “réelles” et d’explorer d’autres modèles comme les SVM ou l’Adaboost. Il nous a aussi fait comprendre l’importance de l’analyse préliminaire et du nettoyage dans la construction d’un modèle d’apprentissage automatique.

Pour aller plus loin, on peut étudier d’autres algorithmes comme la régression logistique ou les analyses discriminantes. De plus, on peut identifier et étudier les zones problématiques pour chaque classifieur et déterminer si certains attributs suivent une distribution particulière dans ces zones. Puis dans un deuxième temps, scinder le jeu de données en partie problématique et non problématique puis appliquer des modèles différentes à chaque partie. Enfin, afin d’obtenir un jeu de données plus représentatif du jeu Pokémon, peut-être que récupérer les résultats de combats réellement joués par des joueurs serait pertinent. Des applications comme “Pokémon Showdown” le permettent.