🇫🇷 METAR data analysis & warehousing with Cassandra
Dans le cadre de ce projet, nous avons construit un stockage orienté colonne destiné à répondre à un ensemble de question sur des données METAR (c’est-à-dire des données météorologiques pour l’aviation). D’une manière plus concrète, notre jeu de données est restreint dans l’espace (exclusivement en Finlande) et dans le temps (entre le 1er Janvier 2004 au 1er Janvier 2014). Puisque dans ce cas, les trois questions ne peuvent pas être répondus par une modélisation commune, nous allons traiter dans ce rapport selon l’ordre des questions.
Prévisualisation du jeu de données
Les données venant de la base de données IEM (Iowa Environmental Mesonet) correspondent à des donnée ASOS (une sous-famille des données METAR) sont constituées de $30$ variables.
Les attributs ${timestamp, longitude, latitude, altitude}$ permettent de définir d’une manière unique un enregistrement, autrement dit, à un instant $t$ donné, à la latitude $lat$, la longitude $long$ et l’altitude $alt$, il ne peut exister qu’une seule observation. L’unicité de l’observation est renforcé par le formattage du timestamp qui est normalisé sur UTC (Universel Temps Coordonné). Dans les sections qui suivent, il est important de noter que toutes les données nulles/absentes sont notées “null” et que les données forment des vecteurs creuses.
Première question
Pour un point donné de l’espace, je veux pouvoir avoir un historique du passé, avec des courbes adaptées. Je vous pouvoir mettre en évidence la saisonnalité et les écarts à la saisonnalité.

Afin de pouvoir identifier un point donné de l’espace, nous pouvons utilisé le tripplet $(long, lat, alt)$. Néanmoins, cette méthode est très restrictive notamment si on veut appliquer cette requête sur une zone dans l’espace. Nous avons donc choisi d’utiliser le geohash. Ce dernier est une fonction de hashage qui subdivise la surface terrestre selon une grille hiérarchique. D’une manière plus concrète, soit $G \subset \mathbb{R}^{2}$ l’ensemble des coordonnées géographiques et $W_p$ l’ensemble des chaînes alphabétiques de longueur $p$ (qui correspond à la précision du geohash), on a:
$$geohash :\quad G \rightarrow W_p$$
$$(lat,lon) \mapsto geohash(lat, lon)\ avec\ len(geohash)=p$$
Néanmoins, mettre l’ensemble du geohash en clé de partitionnement va nous aboutir au même problème d’avoir des partitions trop fines. Puisqu’il s’agit d’un hash hiérarchique, le geohash permet de s’assurer que deux hash commençant par la même lettre sont dans le même pavé, ce qui garantit la cohérence des données vis-à-vis du partitionnement. On peut donc séparer le hash en deux, une partie allant dans la clé de partitionnement (qu’on note $geohash_{key}$), l’autre dans la surclef ($geohash_{part}$). Grâce à l’algorithme de preuve (Voir helper.py), on a déduit qu’avec notre jeu de données, la conception optimale sera :
$$geohash :\quad G \rightarrow W_p$$
$$\quad (lat,lon) \mapsto geohash(lat, lon) = geohash_{key} + geohash_{hash}$$
$$avec\ len(geohash_{key})=2\ et\ len(geohash_{part})=p -2$$
En ce qui concerne l’historique, nous avons choisi de clusteriser selon l’année afin de faciliter la lecture tout en permettant à un partitionnement capable d’évoluer au cours du temps. De plus, étant donné qu’il s’agit d’un historique (c’est-à-dire qu’on cherche toutes les informations depuis une date précise jusqu’à la date actuelle), on peut implémenter des clés de tris du type $mois, jour, heure, seconde$. Néanmoins, cette implémentation pose problème avec l’historique puisque ce dernier nécessite une suite d’opérateurs de comparaison $>$ (interdite par scylla). On a donc concaténé ces valeurs dans un entier $timestamp_{rest}$ qui permettrait cette comparaison.
De plus, afin de pouvoir construire des courbes d’évolution capable de démontrer la saisonnalité, nous avons implémenté des courbes d’évolution des variables quantitatives (par exemple la température ressentie). Finalement, nous avons la conception qui suit;
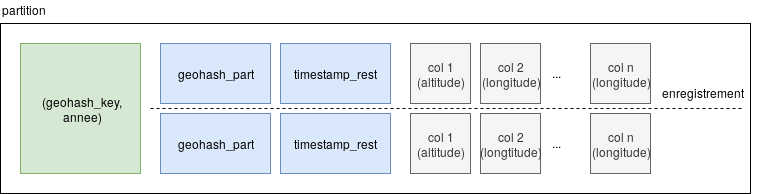
Deuxième question
À un instant donné je veux pouvoir obtenir une carte me représentant n’importe quel indicateur.
Contrairement à la conception précédente, dans cette requête, l’hiérarchie temporelle emporte par rapport à l’hiérarchie géographique. De plus, contrairement à l’historique, la requête porte sur un instant spécifique et non pas une période.
En terme de clé de partition, nous avons choisi d’utiliser un couple $(année, mois)$ afin de constituer un nombre raisonnable de partitions théoriquement homogènes (Avec le jeu de données en question, on aurait $nb_{annee} \times nb_{mois} = 10 \times 12 = 120$ partitions contenant potentiellement de $\underbrace{545791}_\textrm{nb enregis.} / 120 = 4500 $ enregistrements par partition). Pour composer la surclef, on ajoute les attributs heure, minute, seconde (afin de compléter l’hiérarchie temporelle), la longitude, la latitude et l’altitude. L’ordre des clefs de tri permet de requêter la base sans connaître la position exacte de l’observation. Finalement, ceci aboutit à la modélisation qui suit:
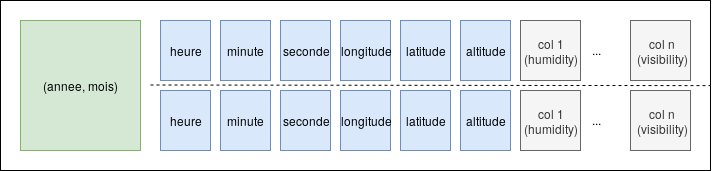
En terme de représentation, nous avons choisi de superposer nos latitudes et nos longitudes sur une carte interactive de la Finlande construite par le module folium. De plus, puisque la question n’impose aucune contrainte d’interprétation, les données en question sont interprétées sous l’angle d’analyse des températures ressenties, c’est-à-dire que pour un instant donné, on veut savoir quelle est la plage de température mesurée à une station donnée. Sur la carte, les températures seront représentées avec des couleurs différentes et les autres indicateurs dans le popup correspondant.
Troisième Question
Pour une période de temps donnée, je veux pouvoir clusteriser l’espace, et représenter cette clusterisation.
Similairement à la question 2, l’hiérarchie temporelle remporte sur l’hiérarchie géographique. Afin de faciliter l’interrogation des données requises, nous avons concaténé les attributs année, mois et jour (afin de constituer un entier sous format YYYYmmdd) pour former une clé de partition. A ceci, s’ajoute les clefs de tri heure et minute qui facilite le requêtage par rapport à une période spécifique d’une journée. Ceci a donc aboutit à la conception suivante:

Afin de clusteriser les données provenant de différentes stations, nous avons choisi d’utiliser l’algorithme des k-means, ce dernier prenant en paramètre un ensemble de colonnes du jeu de donnée et en hyper-paramètre une valeur k entière. Nous avons choisi de l’implémenter sur qu’une seule dimension d’une part par défaut de temps, d’autre part à cause du fait que chaque dimension est indépendante.
L’algorithme précédente appliquée sur la température ambiante entre 01/06/2010 et 01/06/2011 permet de construire le diagramme de Voronoï suivant:
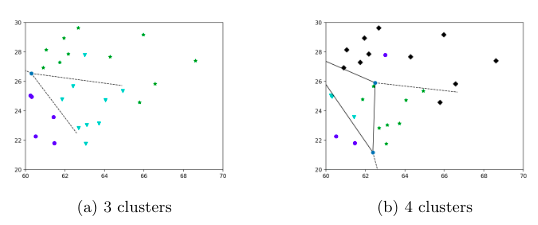
Nous avons choisi de clusteriser avec $k=3$ et $k=4$ pour comparer les résultats. Pour cas $k=3$, on peut distinguer trois groupes qui sont situés au sud, au centre et au nord. C’est logique comme on utilise le température comme le prédicteur, et il dépend fortement de latitude quand le longitude est fixé. Et pour cas $k=4$, on peut voir il a séparé un des trois groupes précédant, et le critique général pour distinguer les clusters est encore le latitude. Pour avoir une vue plus intuitive des clusters, nous les avons projetés sur une carte, les points avec les mêmes couleurs représentent un cluster.
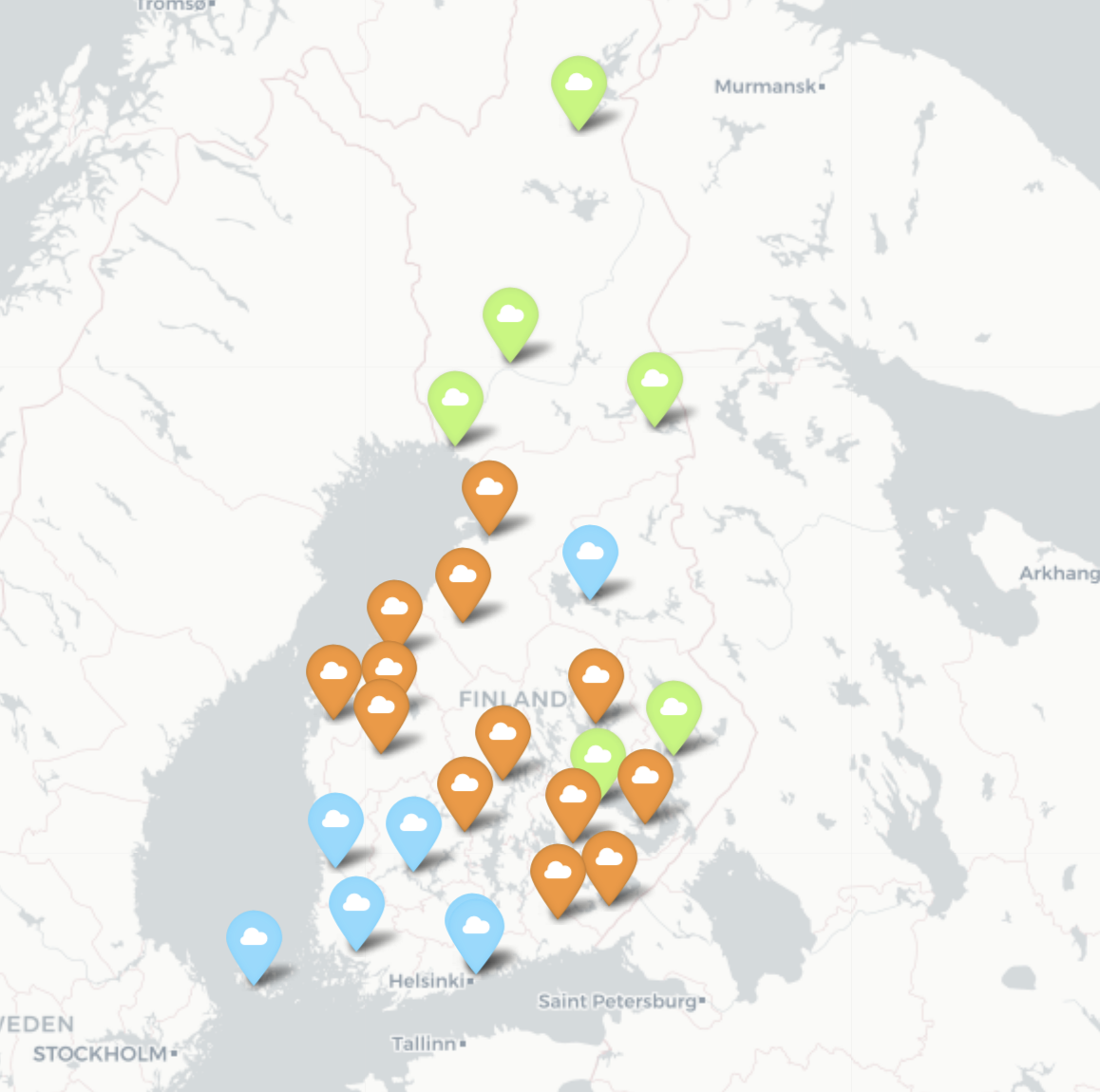
Analyse des performances
Afin d’étudier l’efficacité de notre conception, nous avons effectué une benchmark avec l’ensemble du jeu de donnée chargé sur les trois serveurs qui nous sont attribués. Les indicateurs présentés sont obtenus grâce à la commande:
nodetool tablestats keyspace_name
| SCTS Percentile | Q1 | Q2 | Q3 |
|---|---|---|---|
| SSTable Count | 1 | 3 | 2 |
| Space used | 7.67e6 | 7.51e6 | 3.55e6 |
| SSTable Compression Ration | 0.318 | 0.377 | 0.451 |
| Number of estimated partitions | 76 | 2317 | 2418 |
| Compacted partition mean bytes | 1e6 | 1.3e4 | 5e3 |
| DTCS Percentile | Q1 | Q2 | Q3 |
|---|---|---|---|
| SSTable Count | 2 | 2 | 1 |
| Space used | 3.36e7 | 3.61e7 | 6.45e5 |
| SSTable Compression Ration | 0.317 | 0.377 | 0.496 |
| Number of estimated partitions | 98 | 2379 | 2483 |
| Compacted partition mean bytes | 1.21e6 | 4.35e4 | 5e3 |
| TWCS Percentile | Q1 | Q2 | Q3 |
|---|---|---|---|
| SSTable Count | 1 | 3 | 2 |
| Space used | 3.38e7 | 3.61e7 | 5.37e6 |
| SSTable Compression Ration | 0.32 | 0.378 | 0.48 |
| Number of estimated partitions | 98 | 2379 | 2484 |
| Compacted partition mean bytes | 6.78e5 | 4.3e4 | 5e3 |
Le critère du nombre de SSTable correspond au nombres magasins clé valeur nécessaires pour indexer les contenus de la table en question. En réalité, à chaque écriture, Cassandra écrit la donnée dans une table memtable et un commit log, ces derniers étant mis en mémoire physique (dans une SSTable) une fois un threshold dépassé. Donc plus le nombre de SSTable est important, plus la possibilité qu’une donnée cherchée soit répartie sur plusieurs SSTable, ce qui augmente la latence des lectures réduisant ainsi la performance. Nous observons donc que la latence d’écriture ne fera pas l’objet de notre optimisation.
Le deuxième critère de performance s’agit du ratio de compaction des SSTables correspond à un indicateur sur l’efficacité du stockage en mémoire. La compaction correspond à un rassemblement On observe donc un goulot d’étranglement du système au niveau de la mémoire puisque ce facteur est relativement faible (environ 0.3 - 0.4). Malgré le fait que nos données sont “sparse”, la stratégie de compaction par défaut SizeTieredCompactionStrategy (ne s’applique que lorsqu’un threshold du nombre de SSTable est dépassé) n’est donc pas adaptée. Puisque nos données présentent à chaque fois une dimension temporelle, les stratégies DateTieredCompactionStrategy (DTCS) et TimeWindowCompactionStrategy (TWCS) sont donc plus adaptées (notamment avec la question 3).
Mis à part ces options, notre modélisation peut aussi être remise en question grâce aux données sur le nombre de partitions estimé ainsi que la distribution des données par partition avec la commande :
nodetool cfhistograms keyspace_name.table_name
| Percentile | Q1 Cell Count | Q2 Cell Count | Q3 Cell Count |
|---|---|---|---|
| .5 | 182785 | 446 | 642 |
| .75 | 182785 | 446 | 770 |
| .95 | 263210 | 9887 | 924 |
| .98 | 315852 | 11864 | 1109 |
| .99 | 315852 | 14237 | 1109 |
| min | 35426 | 104 | 2 |
| max | 315852 | 17084 | 1109 |
Il est important de contextualiser le fait que notre jeu de donnée est restreint géographiquement et la modélisation proposée est destinée à être scalable à ce niveau. En terme de distribution, la distribution est relativement homogène puisque les quartiles sont proches. Le nombre de partitions faibles observées à la question 1 et sa distribution confirme donc la validité de notre conception.
De même, les modélisations répondant aux autres questions engendrent la création de 1000 fois plus de partition. Cette différence, malgré énorme peut être expliqué grâce à l’hiérarchie temporelle construite aboutissant à environ 13 partitions par mois. Contrairement à la première conception, celles-ci présentent une distribution fortement hétérogène qui peut, en partie, être expliquée par la distribution des dates des mesures météorologiques. Tout de même, il faudrait remettre en question ces modélisations.
Conclusion
En conclusion, à travers ce projet, nous avons proposé un ensemble de modélisations adaptables avec une interface permettant de les exploiter. Nous avons été confronté à des problématiques de gestion et d’exploitation des données réelles, imparfaites, mal formatées, hétérogènes et parfois inexploitables.
Néanmoins, il reste beaucoup de points à travailler pour que ce dernier peut répondre à des usages en environnement de production. En terme d’améliorations possibles, nous pouvons optimiser les calculs (moyenne, médiane, etc…) et implémenter des algorithmes de Statistical Learning plus approfondie en le distribuant avec Spark. De même par défaut de temps, nous n’avons pas pu construire des outils de visualisation plus intuitive pour exploiter les données, ni optimiser le déploiement avec des paramètres plus avancées (comme par exemple la classe de Compression, la gestion des Tombstones, etc…).